А.Н. Вакилов, М.В. Мамонова, В.В. Прудников, Омский государственный университет, кафедра теоретической физики
При описании адгезионных свойств материалов особенно эффективно полупроводников использован подход, основанный на диэлектрическом формализме. Использование модельных аппроксимаций для диэлектрических функций данных материалов позволяет определить их адгезионные характеристики на основе только концентрации валентных электронов и ширины запрещенной зоны.Возможности данного подхода при его применении к вычислению молекулярных (ван-дер-ваальсовых) сил взаимодействия поверхностей различных тел показаны, например, в работе [3].Ван-дер-ваальсовы силы обуславливают взаимодействие тел при достаточно больших величинах зазора l между их поверхностями  и связаны с корреляционными эффектами взаимодействия посредством флуктуирующего электромагнитного поля, вызванного флуктуациями наведенных дипольных моментов атомов и молекул вещества. При меньших величинах зазора наряду с корреляционной энергией взаимодействия необходимо учитывать флуктуационную составляющую обменной энергии взаимодействия электронов с обменно-коррелляционными дырками. Совместное действие этих обменно-корреляционных эффектов взаимодействия электронов и определяет прежде всего энергию адгезии различных тел как при малых,так и достаточно больших величинах зазора l вплоть до 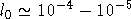 см , где в корреляционной энергии взаимодействия тел необходимо учитывать эффекты запаздывания.В данной работе эффекты запаздывания не учитываются, т.е. считается, что 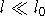 . Основные соотношения теории для обменно-корреляционного взаимодействия флуктуаций электронных плотностей различных тел рассматриваются в длинноволновом приближении.
Рассмотрим взаимодействие между двумя полубесконечными материалами, находящимися при температуре Т=0 К и занимающими области z<0 и z>l. Пренебрежение эффектами запаздывания во взаимодействии тел позволяет в уравнениях Максвелла формально положить 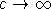 и тем самым использовать уравнение электростатики для потенциала электростатического поля  в данной системе:
 |
(1) |
и получить
 |
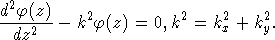(2) |
Нас интересуют решения, имеющие характер коллективных колебаний, локализованных у поверхности (изчезающие при  ). В результате из (2) имеем:
 |
(3) |
Сшивая решения (3) на границе раздела (z=0,l) из условий непрерывности тангенциальной составляющей напряженности электрического поля и нормальной составляющей электрической индукции (эти условия эквивалентны непрерывности  и  ), получаем как условие существования нетривиального решения следущее дисперсионное уравнение для поверхностных волн в системе:
 |
(4) |
Корни этого уравнения и есть интересующие нас собственные частоты поверхностных колебаний.Для их нахождения необходимо задать явный вид функций диэлектрической проницаемости  для 1 и 2 материалов в рамках той или иной принимаемой модели взаимодействия этих сред. Согласно [3], энергия взаимодействия,связанная с наличием поверхностей раздела двух полубесконечных тел,находящихся на расстоянии l (в расчете на единицу площади), равна
 |
(5) |
где функция  задана в (4). Функция  является аналитической функцией везде, кроме конечного числа полюсов 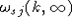 , соответствующих частотам поверхностных волн при  . Нули , равные  , соответствуют частотам поверхностныхволн при произвольных, но конечных l. Согласно принципу аргумента в теории функций комплексного переменного, интеграл  равен разности между полным числом нулей и полюсов функции . В итоге получим
 |
(6) |
Эта формула имеет простой физический смысл: энергия взаимодействия равна разности энергий "нулевых"поверхностных колебаний, когда тела находятся соответственно на расстояниях l и . Нас интересуют коллективные возбуждения электронной системы твердых тел, обусловленные взаимодействием электронов с обменно-корреляционными дырками. Рассмотрим электронную систему в рамках модели "желе", когда заряд электронов каждого из материалов скомпенсирован однородным положительным фоном. Учет обменных и корреляционных эффектов во взаимодействии электронов осуществляется в приближении Хартри-Фока. Коллективные возбуждения электронной системы - плазмоны в длинноволновом приближении математически соответствуют использованию приближения хаотических фаз, в рамках которого диэлектрические проницаемости материалов можно записать в виде [4,5]:
 |
(7) |
где  - соответственно плазменная частота, фермиевская скорость и концентрация электронов валентной зоны n-го материала; Egn - ширина запрещенной зоны этого материала;  -корректирующий множитель,численные коэффициенты в котором обеспечивают стандартную дисперсию объемной плазменной частоты [5]:
 |
(8) |
Для определения закона дисперсии собственных поверхностных плазменных колебаний 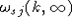, соответствующих величине зазора между материалами l и , необходимо подставить диэлектрические проницаемости материалов из (7) в дисперсионное уравнение (4). Для случая дисперсионное уравнение (4) приводит к соотношениям :
 |
(9) |
определяющим частоты поверхностных плазмонов  на границе раздела n-го материала с вакуумом.Откуда с учетом (7) получаем:
 |
(10) |
Решение дисперсионного уравнения (4) в случае произвольного l приводит к следующим выражениям для поверхностных плазменных частот :
где использованы обозначения j=1,2 , соответствующие в (11) знакам  ,
Для расчета энергии взаимодействия материалов необходимо полученные выражения (10), (11) для  и 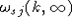подставить в (6) и проинтегрировать по волновым векторам. Но здесь следует учитывать,что поверхностные плазмоны  при некотором критическом значении волнового вектора kc , определяемом условием
 |
(12) |
распадаются, передавая свою энергию и импульс одиночным фермиевским электронам [6]. Это означает,что при k<kc плазмон не может существовать как когерентное движение всех электронов, т.е. он становится практически ненаблюдаемым.Каждая из плазменных мод для различных материалов развязана при и характеризуется своим критическим значением волнового вектора kcn. В связи с этим необходимо в расчетах по формуле (6) проводить интегрирование по волновым векторам k < kcmin , где kcmin соответствует минимальному из значений критических волновых векторов kcn рассматриваемых материалов. Тем самым принимается во внимание вклад во взаимодействие E(l) только коллективных состояний.Энергия адгезии двух различных материалов непосредственно связана с энергией взаимодействия E(l). ТакE (l)= -2Ea(l) [7] и, следовательно,итоговая расчетная формула для энергии адгезии материалов,разделенных зазором l, принимает вид
 |
(13) |
Рис. 2: Энергия адгезии ряда металлов и полупроводников в зависимости от величины вакуумного промежутка l между поверхностями материалов: 1 - Cr-Fe; 2 - Fe-Cu; 3 - Cu-Al; 4 - Ge-ZnS; 5 - Al-InSb.
Рис. 3: Сила адгезии ряда металлов и полупроводников в зависимости от величины вакуумного промежутка l между поверхностями материалов: 1 - Cr-Fe; 2 - Fe-Cu; 3 - Cu-Al;4 - Ge-ZnS; 5 -Al-InSb.
На рис.1 приведены результаты расчета на ПЭВМ энергии адгезии для ряда простых и переходных металлов, а также полупроводников в зависимости от величины зазора l. Для расчета были использованы экспериментальные значения плазменных частот [5].
Сила адгезионного взаимодействия различных материалов как функция величины зазора l между ними может быть получена дифференцированием энергии адгезии Ea12(l) по l, т.е.
 |
(14) |
Следует отметить,что во всем диапазоне изменения l в области применимости теории  сила адгезионного взаимодействия металлов и полупроводников имеет характер притяжения (рис.2). При  электронные системы двух материалов разделены, обменные эффекты при этом несущественны, оставшиеся корреляционные эффекты взаимодействия электронных систем будут соответствовать ван-дер-ваальсовым силам взаимодействия без учета запаздывания [3]. Таким образом они автоматически учитываются в приведенных формулах. В заключении отметим, что использование диэлектрического формализма и представления о поверхностных плазмонах для описания адгезионных свойств различных материалов дает возможность после значительно меньшей по объему вычислительной работы по сравнению с методом функционала плотности получить достаточно корректные результаты, особенно ценные в области достаточно больших величин зазора l, где преобладают ван-дер-ваальсовы силы взаимодействия, учет которых невозможен в рамках метода функционала плотности.
Список литературы
Ухов В.Ф., Кобелева Р.М., Дедков Г.В., Темроков А.И. Электронно-статистическая теория металлов и ионных кристаллов. М.: Наука, 1982. 160 с.
Вакилов А.Н., Потерин Р.В., Прудников В.В., Прудникова М.В. // Физика металлов и металловедение. 1995. Т.79. С.13.
Бараш Ю.С., Гинзбург В.Л. //Успехи физ.наук. 1975. Т.116. Вып.1. С.5.
Неволин В.К., Фазылов Ф.Р., Шермергор Т.Д. //Поверхность. 1983. Т.1. С.79.
Пайнс Д., Нозьер Ф. Теория квантовых жидкостей. М.:Мир, 1967. 384 с.
Платцман Ф., Вольф П. Волны и взаимодействия в плазме твердого тела. М.: Мир, 1975. 440 с.
Wicborg E.C., Inglesfield J.E. //Solid State Comm.1975.V.16.P.335.
|
