Д.Н. Лавров, Омский государственный университет, кафедра математического моделирования
1. Введение
Рассмотрим набор M датчиков, произвольным образом расположенных в пространстве. Дипольная решетка получается из данного набора путем сдвига вдоль вектора h. Вектор h назовем порождающим.
Образуем систему из L дипольных решеток, с каждой из которой ассоциирован порождающий вектор 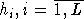 , которую назовем линейной, если система порождающих векторов коллинеарна, плоской - если компланарна, и объемной - в остальных случаях. , которую назовем линейной, если система порождающих векторов коллинеарна, плоской - если компланарна, и объемной - в остальных случаях.
Пусть на эту систему воздействует D плоских волновых фронтов. Каждому из них сопоставлен волновой вектор 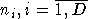 . .
Поставим задачу оценивания компонент волновых векторов по измерениям, полученным от системы дипольных решеток (СДР). Используя метод поворота подпространств [], получим оценки линейных комбинаций типа 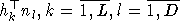 или в матричном виде или в матричном виде

где M -  -матрица измерений фаз; H - -матрица измерений фаз; H - 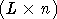 -матрица порождающих векторов, -матрица порождающих векторов, 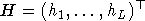 ; N - ; N -  -матрица волновых векторов, -матрица волновых векторов, 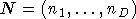 ;где n - размерность волнового вектора, принимаемая за единицу для линейной СДР, n=2 - для плоской и n=3 - для объемной СДР. ;где n - размерность волнового вектора, принимаемая за единицу для линейной СДР, n=2 - для плоской и n=3 - для объемной СДР.
Характерной особенностью метода поворота подпространств является отсутствие информации о глобальной геометрии дипольной решетки, что влечет произвольную перестановку элементов строк матрицы M. Данное обстоятельство обозначим матричным мультииндексом  , представляющим собой целочисленную матрицу, каждая строка которой есть перестановка целых от 1 до D. Таким образом , представляющим собой целочисленную матрицу, каждая строка которой есть перестановка целых от 1 до D. Таким образом

2. Построение оценок
2.1 Оценка наименьших квадратов
Пусть L>n. Рассмотрим матрицу ошибок:

Найдем N, являющуюся решением задачи
 , ,
где

матрица ошибок выписанная по столбцам. Продифференцировав (3) по N (с учетом легко проверяемого свойства  ), приравняв к нулю полученное выражение - для МНК-оценки матрицы волновых векторов получим: ), приравняв к нулю полученное выражение - для МНК-оценки матрицы волновых векторов получим:

Для нахождения  подставим (4) в целевую функцию (3), после простых преобразований имеем подставим (4) в целевую функцию (3), после простых преобразований имеем

где  - проектор на пространство, ортогональное линейной оболочке столбцов H и - проектор на пространство, ортогональное линейной оболочке столбцов H и  . .
Задачу поиска оценки  в дальнейшем будем называть задачей согласования измерений. в дальнейшем будем называть задачей согласования измерений.
2.2 Оценка максимального правдоподобия
Оценки (4) и (5) легко обобщаются, если ошибки измерений  нормально распределены с нулевым средним и нормально распределены с нулевым средним и 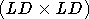 матрицей ковариаций B-1. матрицей ковариаций B-1.
Записав логарифм функции правдоподобия, исключив константы, не зависящие от оцениваемых параметров, приходим к оптимизационной задаче вида

Выражение (2) запишется в виде 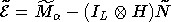 , где IL - , где IL -  -единичная матрица; -единичная матрица; 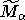 и и 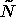 - вектора соответствующих размерностей, полученные из - вектора соответствующих размерностей, полученные из  и N выписыванием компонент по столбцам. Вместо мультииндекса и N выписыванием компонент по столбцам. Вместо мультииндекса  введя введя  матрицу перестановок P, являющуюся произведением матриц элементарных перестановок (причем каждая из этих матриц является допустимой, если переставляет две компоненты матрицу перестановок P, являющуюся произведением матриц элементарных перестановок (причем каждая из этих матриц является допустимой, если переставляет две компоненты 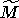 с одинаковыми первыми индексами), получим: с одинаковыми первыми индексами), получим:

Продифференцировав (6) и приравняв нулю полученные производные по 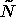 , получим оценку совокупности волновых векторов: , получим оценку совокупности волновых векторов:
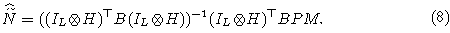
Подставляя (8) в (6), получаем решение задачи согласования

с проектором
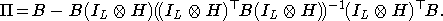
Минимум (9) ищется по всевозможным допустимым матрицам P.
Оценка максимального правдоподобия для одного волнового вектора приведена в []. Выражение (8) является обобщением оценки максимального правдоподобия волновых векторов D-источников излучения.
3. Оптимизация систем дипольных решеток
Будем оптимизировать СДР путем варьирования параметров порождающих векторов, полагая при этом, что длины их равны, тогда без ограничения общности их можно считать единичными. Таким образом, 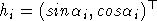 - для плоской решетки и - для плоской решетки и 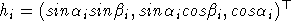 - для объемной решетки. - для объемной решетки.
Известно, что матрица ковариаций МНК-оценки волнового вектора есть 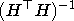 . В качестве числового значения качества оценки можно выбрать любую матричную норму . В качестве числового значения качества оценки можно выбрать любую матричную норму 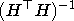 . След симметрической положительно определенной матрицы удовлетворяет всем аксиомам матричной нормы, поэтому в качестве целевой функции выберем . След симметрической положительно определенной матрицы удовлетворяет всем аксиомам матричной нормы, поэтому в качестве целевой функции выберем  . Целевую функцию для плоской решетки обозначим f, а для объемной - g. Имеем: . Целевую функцию для плоской решетки обозначим f, а для объемной - g. Имеем:

где M1, M2, M3 - главные миноры матрицы 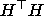 . .
Далее будем использовать свойства целевых функций:
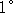 : f, g - инвариантны относительно вращений в пространстве строк H. : f, g - инвариантны относительно вращений в пространстве строк H.
 : f - симметрическая функция своих аргументов (перестановка : f - симметрическая функция своих аргументов (перестановка 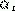 и и 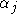 не меняет значения функции). не меняет значения функции).
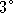 : g - симметрическая функция пар аргументов (перестановка : g - симметрическая функция пар аргументов (перестановка 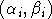 и и 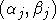 не меняет значения функции). не меняет значения функции).
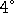 : f, g - периодичны по каждому аргументу. : f, g - периодичны по каждому аргументу.
Используя первое свойство, можно понизить число неизвестных параметров в случае плоской СДР-единицу (положив 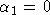 ) и для объемной СДР на три ( ) и для объемной СДР на три ( ). Второе и третье утверждения позволяют сузить область поиска минимума, а также при известном решении получать симметричные ему. ). Второе и третье утверждения позволяют сузить область поиска минимума, а также при известном решении получать симметричные ему.
Вместо минимизации функции f удобнее искать максимумы:

Получим явные выражения для f, градиента  и матрицы Гессе и матрицы Гессе 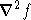 . .

Находя частные производные по 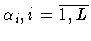 , получим , получим

Матрица Гессе, элементы которой имеют вид:
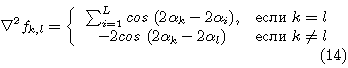
Рассмотрим СДР с минимально возможным количеством дипольных подрешеток (для плоской СДР L=3, для объемной - L=4).
Для случая L=3 (плоская СДР) положим 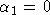 . Линии равного уровня f изображены на рис. 1. Используя (13), запишем систему уравнений . Линии равного уровня f изображены на рис. 1. Используя (13), запишем систему уравнений  в виде в виде

Из всех решений системы
Рис. 1 Целевая функция f (L=3) в квадрате 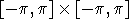 |
 |
существует одно нетривиальное решение: 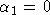 , , 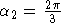 , , 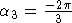 , остальные получаются применением свойств , остальные получаются применением свойств 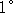 , ,  , , 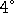 . .
Проверим, что в данной точке 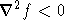 . .

с собственными числами 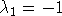 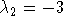 . Так как собственные числа отрицательны, то матрица Гессе отрицательно определена. Таким образом, представленные решения являются точками строгих глобальных максимумов. В частности, также следует, что гексогональные кольцевые решетки оптимальны в смысле минимума целевой функции (10). . Так как собственные числа отрицательны, то матрица Гессе отрицательно определена. Таким образом, представленные решения являются точками строгих глобальных максимумов. В частности, также следует, что гексогональные кольцевые решетки оптимальны в смысле минимума целевой функции (10).
Для объемной СДР (n=3) численная оптимизация методом циклического покоординатного спуска [] для L=4 (с точностью до машинного нуля) приводит к конфигурации векторов hi, образующих правильный тетраэдр, то есть решение задается равенствами:  (в силу свойства (в силу свойства 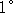 ) ) 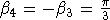 , , 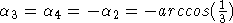 . Вторая конфигурация, к которой сходился алгоритм, получается из первой путем изменения направления какого-либо одного из порождающих векторов. Аналитические вычисления показывают, что градиент в данной точке равен нулю, а матрица Гессе равна: . Вторая конфигурация, к которой сходился алгоритм, получается из первой путем изменения направления какого-либо одного из порождающих векторов. Аналитические вычисления показывают, что градиент в данной точке равен нулю, а матрица Гессе равна:

Характеристический многочлен матрицы имеет вид

с корнями:  , ,  . Так как корни положительны, то положительно определена и матрица Гессе. Следовательно, найдено оптимальное (в смысле минимума (11)) решение. Эксперименты по численной оптимизации не приводят к другим решениям, кроме указанных. Это дает основание полагать, что найденные решения - точки глобальных минимумов g. . Так как корни положительны, то положительно определена и матрица Гессе. Следовательно, найдено оптимальное (в смысле минимума (11)) решение. Эксперименты по численной оптимизации не приводят к другим решениям, кроме указанных. Это дает основание полагать, что найденные решения - точки глобальных минимумов g.
Список литературы
Полрадж А., Рой Р., Кайлатх Т. Оценивание параметров сигнала методом поворота подпространств // ТИИЭР. 1986. Т. 74. N.7. С.165-166.
Белов В.И. Теория фазовых измерительных систем / Под. ред. Г.Н.Глазова. Томск: ТГАСУР, 1994. С.144.
Васильев Ф.П. Численные методы решения экстремальных задач. М.: Гл. ред. физ.-мат. лит., 1988. С. 552.
|