КазиевВ.М.
Рассмотрим пару алгебр (A,B): алгебру X=<X,&,a
(+),a
{},{}a
> событий - алгоритмических процедур (программ) заданную над алфавитом X={x1
,x2
,...,xn
} и В-трехзначную алгебру логики (0,1,2 - неопределенность). В алгебре А определим двухместные операции конъюнкции и условной дизъюнкции и одноместную операцию итерации следующим образом: конъюнкция s1
&s2
событий s1
, s2
состоит из всех слов вида pq, pÎ s1
, qÎ s2
; a - дизъюнкция a
(s1
+s2
) совпадает с s1
(s2
), если условие a истинно (ложно); итерация с постусловием {s}a
состоит из пустого события s0
=e и всевозможных слов вида p1
p2
...pk
т.е. 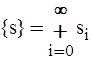 , {s}a
=sm
, где sm
- последний из степеней s, для которого условие a выполнено; итерация с предусловием a
{s} определяется аналогично. В алгебре А задается событие называемое неопределенным и обозначаемое символом Æ. Элементарные события в А - события е, x1
, x2
,..., xn
. Аксиомы алгебры А ниже рассмотрены. Все аксиомы алгебры B и правила вывода в ней сохраняются. Правила вывода, используемые в алгебре А включают правила вывода, принятые в программировании - см., например, [1]. Событие, получаемое применением конечного числа операций алгебры А над элементарными, называется регулярным. , {s}a
=sm
, где sm
- последний из степеней s, для которого условие a выполнено; итерация с предусловием a
{s} определяется аналогично. В алгебре А задается событие называемое неопределенным и обозначаемое символом Æ. Элементарные события в А - события е, x1
, x2
,..., xn
. Аксиомы алгебры А ниже рассмотрены. Все аксиомы алгебры B и правила вывода в ней сохраняются. Правила вывода, используемые в алгебре А включают правила вывода, принятые в программировании - см., например, [1]. Событие, получаемое применением конечного числа операций алгебры А над элементарными, называется регулярным.
Имеет место важная теорема Клини [2]: регулярные события и только они представимы в конечных автоматах.
Рассмотрим задачу построения алгоритма регуляризации во введенной паре алгебр (А,B). Алгоритм в укрупненных шагах состоит в следующем.
Шаг 1. Задается произвольное событие s=s0
s1
s2
...sn+1
, где si
- событие номер i, начальное событие - s0
, конечное - sn+1
, остальные события - преобразователи и/или события - распознаватели.
Шаг 2. Составляется система уравнений алгебры событий А: записывается функция F события, его дерево D и дерево состояний определяющее все к путей выполнения : 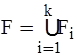 , где Fi
- функция ветви дерева состояний. Функция ветви дерева - композиция всех функций (событий) данной ветви; программная функция F - объединение всех функций ветвей дерева. , где Fi
- функция ветви дерева состояний. Функция ветви дерева - композиция всех функций (событий) данной ветви; программная функция F - объединение всех функций ветвей дерева.
Шаг 3. Система уравнений с помощью подстановок и операций дизъюнкции и конъюнкции представляется в виде : X=XA+B, где X - событие, представленное заключительным состоянием sn+1
,  . .
Шаг 4. Находим решение системы. Используется теорема [3]: если характеристический граф матрицы А (орграф соединяющий ребрами вершины i и j только тогда, когда eÎaij
) не содержит ни одного цикла, то система X=XA+B имеет единственное решение X=B{A}, которое регулярно при регулярных A, B. При решении системы эффективно преобразовывать уравнения, - как и при решении линейных алгебраических уравнений, например, брать дизъюнкцию событий, изменять порядок исключения событий и др.
Шаг 5. По условиям выполнимости событий находим регулярную форму этого решения. Используются аксиомы алгебры логики В и соотношения алгебры событий А, например, следующие (AB=A&B, ab=a&b,a(A) - условие выполнимости события А, Aa - проверка условия a после события А и для этого условия верны все аксиомы алгебры В, 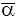 - отрицание условия a): - отрицание условия a):
Ae=eA=A,
ea=a(e)=a,
AÆ=ÆA=Æ,
2
(A+B)=Æ,
a(b(A))=b,
A(BC)=(AB)C,
b
(A+B)=(a(A)+ 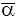 (B)), (B)),
a(b
(A+B))=(ba(A))+(  (B)), (B)),
a
(A+B)C=a
(AC+BC),
Aa
(B+C)=a
(AB+AC),
a(AB)=a(A)Ba(B),
(AB)a=A(Ba),
A{B}a
={BA
a
}A,
a({A}b
)={Ab
}b,
{A}a
=a
(e+A{A}a
),
{a(A)}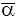 (B)={A} (B)={A}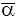 B,
B,
a
{A}a
{A}=a
{A},
{a
a
{A}}=a
{A},
{A}a
{A}a
={A}a
,
{{A}aa
}={A}a
,
{a(A)}={A}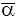 , ,
{A}a
+e=a
{A},
Aa
{A}=a
{A}A={A}a
.
Пример 1. Регуляризуем микропрограмму А деления с фиксированной запятой. Для простоты считаем, что числа неотрицательны, а операция не приводит к переполнению разрядной сетки компьютера фон - Неймановского типа, операционный автомат которого состоит из регистров R1
, R2
сумматора R3
и счетчика сдвигов R4
. Делимое храниться на R1
, делитель - на R2
, частное накапливается на R3
. Введем обозначения: li
- микрооперация сдвига регистра Ri
влево (i=1,2,3); s-1
ij
- микрокоманда вычитания из содержимого регистра Rj
содержимого регистра Ri
; ai
- условие заполненности регистра Ri
; gi
- условие отрицательности содержимого регистра Ri
; pi
- микрооперация занесения единицы в младший разряд Ri
; si,j
- микрокоманда добавления содержимого регистра Ri
к содержимому Rj
.
Выпишем систему уравнений, обозначив через xi
- событие соответствующее каждому из 11 пунктов алгоритма деления (см., например, [3]):
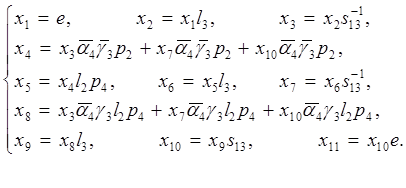
Решим эту систему. После очевидных подстановок, вводя обозначения:
x=x3
+x7
+x10
,
B=el3
s-1
13
,
A=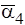 g3
p2
l2
p4
l3
s-1
13
+ g3
p2
l2
p4
l3
s-1
13
+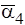 g3
l2
p4
l3
s-1
13 g3
l2
p4
l3
s-1
13
получим уравнение X=XA+B, решение которого будет X=B{A} и после упрощений с помощью приведенных аксиом, заключительное событие S равно
s=x11
l3
s-1
13
{g
3
(l2
p4
l3
s13
+p2
l2
p4
l3
s13
-1
)}a
4
2. Рассмотрим задачу нахождения оптимальных (например, в смысле операции, длины и т.д.) структурированных программ из заданного набора базовых процедур (некоторые из них - см. в [5]), а также построения грамматик для анализа структур из программных единиц. При решении этой задачи используются аксиомы алгебры А.
Пример 2. Дана программа Р, где А,В,С - процедуры, a,b - предикаты:
P=a
(BA+CA)b
(Ab
{A}+e)=a
(B+С)Ab
(Ab
{A}+e)=a
(B+С)Ab
({A}b
+e)=a
(B+С)Ab
{A}=a
(B+C){A}b
=T.
Программа Т - более оптимальна и ее правильность доказываема формально.
Доказана теорема (доказательство не приводим из-за объема).
Теорема 1. Если R,A,S Î A, a,b,gÎB, A и S - коммутативны, то:
а)AX=Aa
(R+SX)ÛAX=A{S}a
R, б)Ag=Aa
(b+Sg)ÛAg=A{S}a
b,
в)Ag=Aa
(b+S 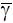 )ÞAg=A{S2
}t
a
(b+S )ÞAg=A{S2
}t
a
(b+S 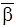 ),t=a+Sa, ),t=a+Sa,
г)Ag=A{S2
}t
gÞAg=At
(e+S2
)g, g=a
(b+S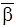 ), t=a+Sa. ), t=a+Sa.
Рассмотрим задачу исследования разрешимости в пространствах программ.
Пусть x=<X, Y, M, S> - программа, определенная на входном алфавите Х, выходном алфавите Y и состоящая из подпрограмм (процедур) М с логической схемой (структурой) S. Структуре S поставим в соответствие орграф: Вершины - подпрограммы, ребра - в соответствии со структурой их взаимодействий. Метрика r(x,y) в этом пространстве - сумма всех весов ребер орграфов программ не совпадающих при заданной структуре S или отклоняющихся от оптимальной структуры, т.е.  Аксиомы метрики проверяемы. Аксиомы метрики проверяемы.
Отметим метризуемость пространства и по некоторым характеристикам качества программ Холстеда [6], а также с помощью понятия интеллектуальной работы программы, оцениваемой как разность энтропии до работы (статической формы программы) и после работы (динамической формы). У идеальной программы энтропия равна нулю. Отметим, что если ds/dt - общее изменение энтропии программного комплекса при отладке, ds1
/dt - изменение энтропии за счет необратимых изменений структуры, потоков внутри комплекса (рассматриваемую как открытую систему), ds2
/dt - изменение энтропии за счет усилий по отладке и тестированию, то справедливо уравнение Пригожина: ds/dt = ds1
/dt + ds2
/dt. Последовательность программ {xi
}, сходится по схеме (структуре) к программе х (обозначим 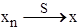 ), если r(xn
,x)® 0, при n®¥, т.е. дерево программы xn
при n®¥ стремится к дереву программы х. Последовательность {xi
} сходится функционально к программе х (обозначим ), если r(xn
,x)® 0, при n®¥, т.е. дерево программы xn
при n®¥ стремится к дереву программы х. Последовательность {xi
} сходится функционально к программе х (обозначим 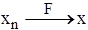 ), если F(xn
)® F(x) при n®¥ (программная функция xn
стремится к программной функции х). Нетрудно видеть, что из сходимости по схеме следует сходимость функциональная, но обратное неверно. ), если F(xn
)® F(x) при n®¥ (программная функция xn
стремится к программной функции х). Нетрудно видеть, что из сходимости по схеме следует сходимость функциональная, но обратное неверно.
Пусть M = {x1
, x2
, ..., xn
,...} - последовательность программ с общей функцией (эквивалентных функционально). На этом множестве рассмотрим множество операторов А преобразования (композиции, суперпозиции) программ. Последовательность {An
} сходится к А функционально (по схеме, структуре), если верно: "xÎМ: 
С точки зрения исследования существования, единственности оптимальной (в каком-то смысле) программы можно рассмотреть: операторы минимизации числа операндов; операторы минимизации числа типов операторов; операторы минимизации числа вызовов процедур; минимизации числа ошибок в программе; минимизации сложности (разных способов определения) и др. При исследовании программных систем важно рассматривать пространства векторов х=(х1
,x2
,...,xn
), где xi
- характеристика ошибок в программе или структурной связностипроцедур, ui
- количество ошибок в i-ом модуле программного комплекса P(u)=P(u1
,u2
,...,un
).
Пусть u(x,t) - количество ошибок, обнаруженных в программе (системе) в момент времени t, а х - характеристика уровня ошибок. Рассмотрим модель обнаружения ошибок при отладке, представимая уравнением (см. также [7]): Lu+Tu=f, где T - оператор, определяющий первоначальный уровень ошибок в программе или их некоторую характеристику, L - некоторый линейный ограниченный оператор отладки, L:U®V, U,V - линейные нормированные пространства D(L) ÍU, R(L)ÍV.
Теорема 2. Если R(L)=V и для каждого uÎD(L) существует постоянная c такая, что  , то Lu+Tu=f имеет единственное решение uÎU. , то Lu+Tu=f имеет единственное решение uÎU.
Доказательство. Условия теоремы гарантируют существование непрерывного обратного оператора L-1
, причем 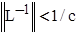 . Тогда u=L-1
(f-Tu). Для однородного уравнения: . Тогда u=L-1
(f-Tu). Для однородного уравнения: 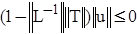 . Отсюда следует, что . Отсюда следует, что  , т.е. u=0. Следовательно, неоднородное уравнение имеет единственное решение. , т.е. u=0. Следовательно, неоднородное уравнение имеет единственное решение.
Пример 3. Пусть umax
- максимальный уровень синтаксических ошибок в программе Р, u(t) - их оставшееся количество к моменту времени t. Исходя из модели du/dt+lumax
=0, u(t0
)=u0
можно заключить, что уровень ошибок убывает при l(c-t0
) ¹ -1 (t0
<c<T) по закону: u(t) = u0
(1+ l(c-t))/(1+l(c-t0
)).
Если задать дополнительно u(t*
)=u*
, (umax
- неизвестная величина), то закон изменения уровня ошибок находится однозначно, так как: с=(u*
t0
-u0
t*
)/(lu*
-lu0
)-1/l.
Вопросы разрешимости некоторых уравнений Lx=y, где х - неизвестная программа, y - заданная программа, L - оператор, например, оптимизации, будут изложены в другой работе.
Список литературы
1. Алагич С., Арбиб М. Проектирование корректных структурированных программ. - М., Радио и связь, 1984.
2. Клини С.К. Представление событий в нервных сетях и конечных автоматах. - Автоматы, ИЛ, М., 1956.
3. Бондарчук В.Г. Системы уравнений в алгебре событий. - Журнал вычислительной математики и математической физики, N6, т.3, 1963.
4. Глушков В.М. О применении абстрактной теории автоматов для минимизации микропрограмм. - Изв. АН СССР, Технич. кибернетика, N1, 1964.
5. Казиев В.М. Дидактические алгоритмические единицы. - Информатика и образование, N5, 1991.
6. Холстед М. Начала науки о программах. - М., Финансы и статистика, 1981.
7. Казиев В.М. Один класс математических моделей переработки информации и некоторые его приложения. - Нелинейные эволюционные уравнения в прикладных задачах, Киев, 1991.
|