 Міністерство освіти України
ДАЛПУ
Кафедра автоматизації
технологічних процесів і приладобудування
КУРСОВА РОБОТА
з курсу
“Математичне моделювання на ЕОМ”
на тему
“Розв’язок диференціального рівняння
виду ап
у(п)
+ап-1
у(п-1)
+…+а1
у1
+а0
у=кх при заданих
початкових умовах з автоматичним вибором кроку
методом Ейлера”
Виконала студентка групи БА-4-97
Богданова Ольга Олександрівна
Холоденко Вероніка Миколаївна
Перевірила Заргун Валентина Василівна
1998
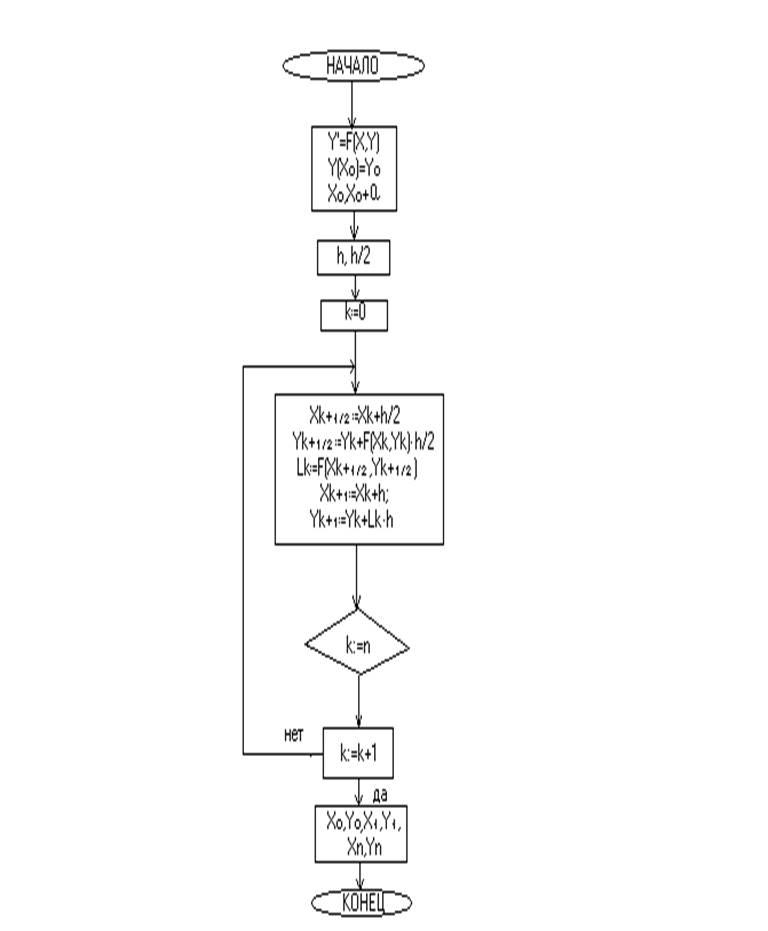
Блок-схема алгоритма
Блок-схема алгоритма
 начало
 у
/
=f(x,y)
y(x0
)=y0
x0
,
x0
+a
h, h/2
k:=0
 xk+1/2
:=xk
+h/2
yk+1/2
:=yk
+f(xk,
yk
)h/2
αk
:=f(xk+1/2,
yk+1/2
)
xk+1
:=xk
+h
yk+1
:=yk
+αk
h
   нет
k:=n
 да
 x0
,
y0
,
x1
,
y1…
xn
,
yn
 конец
ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ
Решить дифференциальное уравнение у/
=f(x,y) численным методом - это значит для заданной последовательности аргументов х0
, х1
…, хn
и числа у0
, не определяя функцию у=F(x), найти такие значения у1
, у2
,…, уn
, что уi
=F(xi
)(i=1,2,…, n) и F(x0
)=y0
.
Таким образом, численные методы позволяют вместо нахождения функции
У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk
-xk
-1
называется шагом интегрирования.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка
y/
=f(x,y) (1)
с начальным условием
x=x0
, y(x0
)=y0
(2)
Требуется найти решение уравнения (1) на отрезке [а,b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0
, х1
, х2
,…, хn
, где xi
=x0
+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi
)»yi
вычисляются последовательно по формулам уi
+hf(xi
, yi
) (i=0,1,2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М0
(х0
, у0
), заменяется ломаной М0
М1
М2
… с вершинами Мi
(xi
, yi
) (i=0,1,2,…); каждое звено Мi
Mi+1
этой ломаной, называемой ломаной Эйлера,
имеет направление, совпадающее с направлением той интегральной кривой уравнения (1), которая проходит через точку Мi
.
Если правая часть уравнения (1) в некотором прямоугольнике R{|x-x0
|£a, |y-y0
|£b}удовлетворяет условиям:
|f(x, y1
)- f(x, y2
)| £ N|y1
-y2
| (N=const),
|df/dx|=|df/dx+f(df/dy)| £ M (M=const),
то имеет место следующая оценка погрешности:
|y(xn
)-yn
| £ hM/2N[(1+hN)n
-1], (3)
где у(хn
)-значение точного решения уравнения(1) при х=хn
, а уn
- приближенное значение, полученное на n-ом шаге.
Формула (3) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет
: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагомh/2. Погрешность более точного значения уn
*
оценивается формулой
|yn
-y(xn
)|»|yn
*
-yn
|.
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.
Модифицированный метод Эйлера
более точен.
Рассмотрим дифференциальное уравнение (1) y/
=f(x,y)
с начальным условием y(x0
)=y0
. Разобьем наш участок интегрирования на n
 равных частей.На малом участке [x0
,x0
+h]
у
интегральную кривую заменим прямой
    Nk
/
y=y(x)
линией. Получаем точку Мк
(хк
,ук
).
 
      Мк
Мк
/
  yk+1
  yk
 хк
хк1
/2
xk+h=
xk1
х
Через Мк
проводим касательную: у=ук
=f(xk
,yk
)(x-xk
).
Делим отрезок (хк
,хк1
) пополам:
xNk
/
=xk
+h/2=xk+1/2
yNk
/
=yk
+f(xk
,yk
)h/2=yk
+yk+1/2
Получаем точку Nk
/
. В этой точке строим следующую касательную:
y(xk+1/2
)=f(xk+1/2
, yk+1/2
)=αk
Из точки Мк
проводим прямую с угловым коэффициентом αк
и определяем точку пересечения этой прямой с прямой Хк1
. Получаем точку Мк
/
. В качестве ук+1
принимаем ординату точки Мк
/
. Тогда:
ук+1
=ук
+αк
h
xk+1
=xk
+h
(4) αk
=f(xk+h/2
, yk
+f(xk
,Yk
)h/2)
yk
=yk-1
+f(xk-1
,yk-1
)h
(4)-рекурентные формулы метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции ук+1
/
2
в точках хк+1
/2
, затем находят значение правой части уравнения (1) в средней точке y/
k
+1
/2
=f(xk+1/2
, yk+1/2
) и определяют ук+1
.
Для оценки погрешности в точке хк
проводят вычисления ук
с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений:
| ук
*
-у(хк
)|=1/3(yk
*
-yk
),
где у(х)-точное решение дифференциального уравнения.
Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y//
=f(y/
,y,x) c начальными условиями y/
(x0
)=y/
0
, y(x0
)=y0
, выполняется замена:
y/
=z
z/
=f(x,y,z)
Тем самым преобразуются начальные условия:y(x0
)=y0
, z(x0
)=z0
, z0
=y/
0
.
РЕШЕНИЕ КОНТРОЛЬНОГО ПРИМЕРА
Приведем расчет дифференциального уравнения первого, второго и третьего порядка методом Эйлера
1
. Пусть дано дифференциальное уравнение первого порядка:
y/
=2x-y
Требуется найти решение на отрезке [0,1] c шагом h=(1-0)/5=0,2
Начальные условия: у0
=1;
Пользуясь рекурентными формулами (4), находим:
1). x1
=0,2; х1
/2
=0,1; y(x1
)=y(x0
)+α0
h; y(x1/2
)=y(x0
)+f(x0
,y0
)h/2;
f(x0
,y0
)=2*0-1=-1
y(x1/2
)=1-1*0,1=0,9
α0
=2*0,1-0,9=-0,7
y1
=1-0,1*0,2=0,86
2). y(x2
)=y(x1
)+α1
h; x2
=0,2+0,2=0,4; x1+1/2
=x1
+h/2=0,2+0,1=0,3
y(x1+1/2
)=y(x1
)+f(x1
,y(x1
))h/2
f(x1
,y1
)=2*0,2-0,86=-0,46
y(x1+1/2
)=0,86-0,46*0,1=0,814
α1
=2*0,3-0,814=-0,214
y2
=0,86-0,214*0,2=0,8172
3). x3
=0,4+0,2=0,6; x2+1/2
=x2
+h/2=0,4+0,1=0,5
f(x2
,y2
)=2*0,4-0,8172=-0,0172
y2+1/2
=0,8172-0,0172*0,1=0,81548
α2
=2*0,5-0,81548=0,18452
y3
=0,8172+0,18452*0,2=0,854104
4).x4
=0,8; x3+1/2
=x3
+h/2=0,6+0,1=0,7
f(x3
,y3
)=2*0,6-0,854104=0,345896
y3+1/2
=0,854104+0,345896*0,1=0,8886936
α3
=2*0,7-0,89=0,5113064
y4
=0,854104+0,5113064*0,2=0,95636528
5).x5
=1; x4+1/2
=0,8+0,1=0,9
f(x4
,y4
)=2*0,8-0,956=0,64363472
y4+1/2
=0,956+0,643*0,1=1,020728752;
α4
=2*0,9-1,02=0,779271248
y5
=0,956+0,7792*0,2=1,11221953
2
. Дано уравнение второго порядка:
y//
=2x-y+y/
Находим решение на том же отрезке [0,1] c шагом h=0,2;
Замена: y/
=z
z/
=2x-y+z
Начальные условия: у0
=1
z0
=1
1).x1
=0,2; x1/2
=0,1
y(z1
)=y(z0
)+α0
h z(x1
,y1
)=z(x0
,y0
)+β0
h
y(z1/2
)=y(z0
)+f(z0
,y0
)h/2 z(x1/2
,y1/2
)=z(x0
,y0
)+f(x0
,y0
,z0
)h/2
f(z0
,y0
)=f10
=1 f(x0
,y0
,z0
)=f20
=2*0-1+1=0
y1/2
=1+1*0,1=1,1 z1/2
=1+0*0,1=1
α0
=z0
=1 β0
=2*0,1-1,1+1=0,1
y1
=1+0,2*1=1,2
z1
=1+0,2*0,1=1,02
2).x2
+0,4; x1+1/2
=0,3
f11
=z1
=1,02 f21
=2*0,2-1,2+1,02=0,22
y1+1/2
=1,2+1,02*0,1=1,1 z1+1/2
=1,02+0,22*0,1=1,042
α1
=z1+1/2
=1,042 β1
=2*0,3-1,302+1,042=0,34
y2
=1,2+1,042*0,2=1,4084
z2
=1.02+0,34*0,2=1,088
3).x3
=0,6; x2+1/2
=0,5
f12
=z2
=1,088 f22
=2*0,4-1,4084+1,088=0,4796
y2+1/2
=1,4084+1,088*0,1=1,5172 z2+1/2
=1,088+0,4796*0,1=1,13596
α2
=z2+1/2
=1,13596 β2
=2*0,5-1,5172+1,13596=0,61876
y3
=1,4084+1,136*0,2=1,635592
z3
=1,088+0,61876*0,2=1,211752
4).x4
=0,8; x3+1/2
=0,7
f13
=z3
=1,211752 f23
=2*0,6-1,636+1,212=0,77616
y3+1/2
=1,636+1,212*0,1=1,7567672 z3+1/2
=1,212+0,776*0,1=1,289368
α3
=z3+1/2
=1,289368 β3
=2*0,7-1,7568+1,289=0,9326008
y4
=1,6+1,289*0,2=1,8934656
z4
=1,212+0,93*0,2=1,39827216
5).x5
=1; y4+1/2
=0,9
f14
=z4
=1,39827216 f24
=2*0,8-1,893+1,398=1,10480656
y4+1/2
=1,893+1,398*0,1=2,0332928 z4+1/2
=1,398+1,105*0,1=1,508752816
α4
=z4+1/2
=1,508752816 β4
=2*0,9-2,03+1,5=1,27546
y5
=1,893+1,5*0,2=2,195216163
z5
=1,398+1,275*0,2=1,65336416
3
. Чтобы решитьуравнение третьего порядка
y///
=2x-y-y/
+y//
на отрезке [0,1], с шагом h=0,2 и начальными условиями
y0
//
=1
y0
/
=1
y0
=1
необходимо сделать 3 замены: y/
=a y0
/
=a0
=1
y//
=a/
=b y0
//
=b0
=1
b/
=2x-y-a+b
1).x1
=0,2; x1/2
=0,1
y(a1
)=y(a0
)+a0
h y(a1/2
)=y(a0
)+f10
h/2
a(b1
)=a(b0
)+β0
h a(b1/2
)=a(b0
)+f20
h/2
b(x1
,y1
,a1
)=b(x0
,y0
,a0
)+γ0
h b(x1/2
,y1/2
,a1/2
)=b(x0
,y0
,a0
)+f30
h/2
f10
=f(a0
,y(a0
))=1 y1/2
=1+1*0,1=1,1
f20
=f(b0
,a(b0
))=1 a1/2
=1+1*0,1=1,1
f30
=f(x0
,y0
,a0
,b0
)=-1 b1/2
=1-1*0,1=0,9
α0
=a1/2
=1,1 y(a1
)=1+1,1*0,2=1,22
β0
=b1/2
=0,9 a(b1
)=1+0,9*0,2=1,18
γ0
=2*0,1-1,1-1,1+0,9=-1,1 b(x1
,y1
,a1
)=1-1,1*0,2=0,78
2).x2
=0,4; x1+1/2
=x1
+h/2=0,3
f11
=a1
=1,18 y1+1/2
=1,22+1,18*0,1=1.338
f21
=b1
=0,78 a1+1/2
=1,18+0,78*0,1=1,258
f31
=2*0,2-1,22-1,18+0,78=-1,22 b1+1/2
=-1,22*0,1+0,78=0,658
α1
=a1+1/2
=1,258 y2
=1,22+1,258*0,2=1,4716
β1
=b1+1/2
=0,658 a2
=1,18+0,658*0,2=1,3116
γ1
=2*0,3-1,338-1,258+0,658=-1,338 b2
=0,78-1,338*0,2=0,5124
3).x3
=0,6; x2+1/2
=0,5
f12
=a2
=1,3116 y2+1/2
=1,47+1,3*0,1=1,60276
f22
=b2
=0,5124 a2+1/2
=1,3116+0,5*0,1=1.36284
f32
=2*0,4-1,47-1,31+0,512=-1,4708 b2+1/2
=0,4-1,4*0,1=0,36542
α2
=1,36284 y3
=1,4716+1,3116*0,2=1,744168
β2
=0,36542 a3
=1,3116+0,3654*0,2=1,384664
γ2
=2*0,5-1,6-1,36+0,365=-1,60018 b3
= 0,51-1,60018*0,2=0,192364
4).x4
=0,8; x3+1/2
=0,7
f13
=1,384664 y3+1/2
=1,74+1,38*0,1=1,8826364
f23
=0,192364 a3+1/2
=1,38+0,19*0,1=1,4039204
f33
=2*0,6-1,7-1,38+0,19=-1,736488 b3+1/2
=0,19-1,7*0,1=0,0187152
α3
=1,4039204 y4
=1,74+1,4*0,2=2,0249477
β3
=0,0187152 a4
=1,38+0,9187*0,2=1,388403
γ3
=2*0,7-1,88-1,4+0,0187=-1,8678416 b4
=0,192-1,87*0,2=-0,1812235
5).x4
=1; x4+1/2
=0,9
f14
=1,388403 y4+1/2
=2,02+1,388*0,1=2,16379478
f24
=-0,1812235 a4+1/2
=1,4-0.181*0,1=1,370306608
f34
=2*0,8-2,02-1,388-0,18=-1,9945834 b4+1/2
=-0,18-1,99*0,1=-0,38066266
α4
=1,3703 y5
=2,02+1,37*0,2=2,2990038
β4
=-0,38066 a5
=1,388-0,38*0,2=1,3122669
γ4
=2*0,9-2,16-1,37-0,38=-2,114764056 b5
=-0,181-2,1*0,2=-0,6041734
Программа на
Turbo Pascal
uses crt,pram,kurs1_1;
var
yx,xy,l,v,p,ff,ay,by,x:array [0..10] of real;
y,a,b:array[0..10,0..1] of real;
i,n,o:integer;
c,d,h,k:real;
label
lap1;
begin
screen1;
clrscr;
writeln('введите наивысший порядок производной не больше трех ');
readln(n);
if n=0 then begin
writeln('это прямолинейная зависимость и решается без метода Эйлера ');
goto lap1;end;
writeln('введите коэффициенты {a0,a1}');
for i:=0 to n do
readln(l[i]);
if (n=1) and (l[1]=0) or (n=2) and (l[2]=0) or (n=3) and (l[3]=0) then begin
writeln('деление на ноль');
goto lap1;
end;
writeln('введите коэффициент при x');
readln(k);
writeln('введите отрезок ');
readln(c,d);
o:=5;
h:=abs(d-c)/o;
writeln('шаг=',h:1:1);
writeln('задайте начальные условия y(x)=');
for i:=0 to n-1 do
readln(v[i]);
if n=3 then begin
yx[0]:=v[0];
ay[0]:=v[1];
by[0]:=v[2];
p[0]:=(k*c-l[0]*v[0]-l[1]*v[1]-l[2]*v[2])/l[3];
x[0]:=c;
gotoxy(32,1);
 write('');
gotoxy(32,2);
write(' x y a b ');
gotoxy(32,3);
write('',c:7:7,' ',yx[0]:7:7,' ',ay[0]:7:7,' ',by[0]:7:7,' ');
for i:=0 to o-1 do begin
x[i]:=x[i]+h/2;
y[i,1]:=yx[i]+(h/2)*ay[i];
a[i,1]:=ay[i]+(h/2)*by[i];
b[i,1]:=by[i]+(h/2)*p[i];
ff[i]:=(k*x[i]-l[0]*y[i,1]-l[1]*a[i,1]-l[2]*b[i,1])/l[3];
xy[i]:=x[i]+h/2;
yx[i+1]:=yx[i]+h*a[i,1];
ay[i+1]:=ay[i]+h*b[i,1];
by[i+1]:=by[i]+h*ff[i];
x[i+1]:=x[i]+h/2;
p[i+1]:=(k*xy[i]-l[0]*yx[i+1]-l[1]*ay[i+1]-l[2]*by[i+1])/l[3];
end;
for i:=0 to o-1 do begin
gotoxy(32,4+i);
write(' ',xy[i]:7:7,' ',yx[i+1]:7:7,' ',ay[i+1]:7:7,' ',by[i+1]:7:7,' ');
end;
gotoxy(32,4+o);
 write(' ');
end;
if n=2 then begin
x[0]:=c;
yx[0]:=v[0];
ay[0]:=v[1];
p[0]:=(k*c-l[0]*yx[0]-l[1]*v[1])/l[2];
gotoxy(32,1);
 write(' ');
gotoxy(32,2);
write(' x y a ');
gotoxy(32,3);
write(' ',c:7:7,' ',yx[0]:7:7,' ',ay[0]:7:7,' ');
for i:=0 to o-1 do begin
x[i]:=x[i]+h/2;
y[i,1]:=yx[i]+(h/2)*ay[i];
a[i,1]:=ay[i]+(h/2)*p[i];
ff[i]:=(k*x[i]-l[0]*y[i,1]-l[1]*a[i,1])/l[2];
xy[i]:=x[i]+h/2;
yx[i+1]:=yx[i]+h*a[i,1];
ay[i+1]:=ay[i]+h*ff[i];
x[i+1]:=x[i]+h/2;
p[i+1]:=(k*xy[i]-l[0]*yx[i+1]-l[1]*ay[i+1])/l[2];
end;
for i:=0 to o-1 do begin
gotoxy(32,4+i);
write(' ',xy[i]:7:7,' ',yx[i+1]:7:7,' ',ay[I+1]:7:7,' ');
end;
gotoxy(32,4+o);
 write(' ');
end;
if n=1 then begin
x[0]:=c;
yx[0]:=v[0];
p[0]:=(k*x[0]-l[0]*yx[0])/l[1];
for i:=0 to o-1 do begin
x[i]:=x[i]+h/2;
y[i,1]:=yx[i]+(h/2)*p[i];
xy[i]:=x[i]+h/2;
ff[i]:=(k*x[i]-l[0]*y[i,1])/l[1];
yx[i+1]:=yx[i]+h*ff[i];
x[i+1]:=x[i]+h/2;
p[i+1]:=(k*xy[i]-l[0]*yx[i+1])/l[1];
end;
gotoxy(32,1);
 write(' ');
gotoxy(32,2);
write(' x y ');
gotoxy(32,3);
write(' ',c:7:7,' ',yx[0]:7:7,' ');
for i:=0 to o-1 do begin
gotoxy(32,4+i);
write(' ',xy[i]:7:7,' ',yx[i+1]:7:7,' ');
end;
gotoxy(32,o+4);
write(' ');
end;
lap1:readln;
pramo;
delay(10000);
clrscr;
end.
_
ЗАПУСК ПРОГРАММЫ НА ВЫПОЛНЕНИЕ
Программа находится в файле kursova1.pas, и имеет 2 модуля, в которых содержатся заставки. Модули находятся в файлах pram.tpu и kurs1_1.tpu.
Для запуска файла kursova1.pas в Turbo Pascal необходимо нажать F9. Появится первая заставка, далее нажать enter и ввести все необходимые начальные условия: порядок производной, коэффициенты при членах рада, отрезок и начальные значения у(х0
). На экране выводится шаг вычисления и таблица с ответами. После нажатия enter выводится вторая заставка, после чего мы возвращаемся к тексту программы.
ОПИСАНИЕ ПРОГРАММЫ
1
– ввод данных, используемых в программе
2
– использование метки, очистка экрана, ввод требований, решение
дифференциального уравнения в зависимости от ввода начальных
условий
3
– присвоение начальных условий для дифференциального уравнения
третьего порядка
4
– вывод таблицы со значениями
5
– ввод формул метода Эйлера для уравнения третьего порядка
6
– присвоение начальных условий для решения дифференциального
уравнения второго порядка
7
– вывод таблицы для уравнения второго порядка
8
– формулы метода Эйлера для уравнения второго порядка
9
– начальные условия для дифференциального уравнения первого порядка
10
– формулы метода Эйлера для решения уравнения первого порядка
11
– вывод таблицы
12
– обращение к метке, задержка для просмотра результатов, очистка
экрана, конец программы.
|
