.
С.В. Усатиков, кандидат физ-мат наук, доцент; С.П. Грушевский, кандидат физ-мат наук, доцент; М.М. Кириченко, кандидат социологических наук
Впервые нормальный закон был обнаружен в Х1Х веке в применении к теории ошибок измерения Лапласом и Гаусcом. Сейчас, после доказанной Ляпуповым центральной предельной теоремы, стало уже ясным, почему этот нормальный закон широко распространен в технике, биологии, социологии, психологии и многих других сферах человеческих знаний. Все его содержание показано на рисунке 1, на графике плотности распределения вероятностей.
Рис.1

Рис.1 Плотность распределения вероятностей нормального закона
1,2 - графики с одним средним m и разными стандартными отклонениями s , причем s 1<s 2
3 - график при m =0, s =1 для Z - закона и примерным распределением площадей под кривой.
Под аргументом x здесь можно понимать самые различные числовые величины, не поддающиеся предсказанию до проведения эксперимента: рост, вес, число ошибок при тестировании, умственное развитие, склонность к правонарушениям и любые другие, возникающие как результат сложения многих независимых (или слабо зависимых) и сравнимых по порядку своего влияния случайных воздействий. Функция f(x) показывает следующую важнейшую информацию: вероятность числовой величине х принять значение больше числа а и меньше числа в равна площади под кривой f(x) на отрезке [ a,b] (рис.1). Разумеется, это касается любых a и b, близких между собой или далеких, расположенных в любом месте прямой х. Кроме того, площадь под всей кривой f(x) равна 1, т.е. вероятность для х попасть на прямую равна 1, и это событие достоверное (это свойство еще называется условием нормировки).
У нормального закона два параметра, полностью его определяющих: числа m и s . Число m есть средняя величина для интересующих нас числовых показателей: средний рост, средний вес и т.п. Меняя m , можно т совершать параллельный перенос кривой f(x) вдоль оси х. Видно также, что наиболее вероятно появление числа х в эксперименте вблизи m : площадь под f(x)на любом отрезке, содержащем m, самая большая.
Число s есть среднее отклонение числового показателя х от числа m: чем меньше s , тем “круче” становится “холм” f(x) (рис.1) и тем меньше вероятность для х сильно отличаться от m. Наоборот, при больших s “холм” f(x) растекается по “равнине” и с почти равной вероятностью х может появиться как вблизи m , так и сколь угодно далеко от m.
Если числовой показатель х пересчитать в число Z по следующему правилу:

то все “холмы” f(x) превратятся в кривую 3 закона Z Гаусса на рис.1. Тогда все точки ± 1 для Z соответствует точкам m± s для х, а точки ± 3 для Z - точкам m± 3s для х. По распределению площадей под кривой 3 видно, что на отрезке [ -3,3] сосредоточено примерно 99,7% всей площади под кривой f(x). Отсюда вытекает так называемое правило “трех s “ для закона Z: с вероятностью р=0,997 случайная величина х отклоняется от то все “холмы” f(x) превратятся в кривую 3 закона Z на рис.1. Тогда все точки ± 1 средней m (влево или вправо) не более чем на 3s .
Теперь настал момент объяснить, почему так много внимания уделяется “холму” f(x) на рис.1. В теории вероятностей доказана теорема, совершенно справедливо названная центральной предельной теоремой. В грубых чертах, сумма большого числа (практически более 7 - 10) независимых случайных величин, сравнимых по порядку своего влияния на рассеивание суммы, подчиняется нормальному закону. Например, рост человека, на который оказывают влияние очень много факторов, среди которых в массе нет доминирующих по своему влиянию.
С начала ХХ века оказался очень полезным введенный Пирсоном закон c 2 (рис.2): в страховом деле, в выяснении торгового спроса или популярности политиков и т.п.
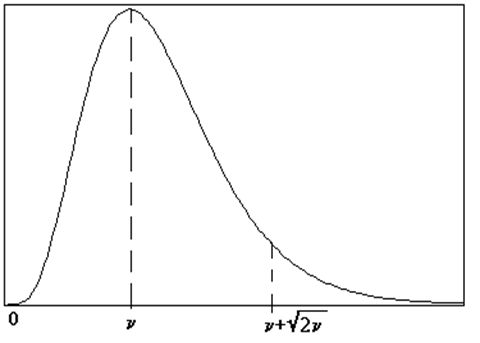
Рис.2. Плотность распределения вероятностей законаc 2, с n степенями свободы.
Под аргументом х здесь понимается сумма n независимых слагаемых в квадрате, каждое из которых подчиняется нормальному Z- закону с m =0 и s =1. Ясно, что при больших n (практически при n >30) закон c 2 превращается в нормальный закон с m = n и s =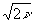 , поскольку действует теорема Ляпунова. Но чаще всего слагаемых не более 10. Число n называеся числом степеней свободы. Смысл f(x) такой же, как и в нормальном законе: вероятность числовой величине х=c 2 попасть в заданный диапазон равна площади под кривой f(x). Так, площадь под кривой на отрезке от 0 до n + , поскольку действует теорема Ляпунова. Но чаще всего слагаемых не более 10. Число n называеся числом степеней свободы. Смысл f(x) такой же, как и в нормальном законе: вероятность числовой величине х=c 2 попасть в заданный диапазон равна площади под кривой f(x). Так, площадь под кривой на отрезке от 0 до n +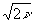 составляет более 90% всей площади под всей кривой f(x). Отсюда следут правило “трех s “ для закона c 2: с вероятностью рі 0,9 случайная величина х=c 2 не превосходит величины n +Ц 2n (очевидно, c 2 не может быть отрицательным). составляет более 90% всей площади под всей кривой f(x). Отсюда следут правило “трех s “ для закона c 2: с вероятностью рі 0,9 случайная величина х=c 2 не превосходит величины n +Ц 2n (очевидно, c 2 не может быть отрицательным).
Наконец, необходимо упомянуть закон t Стьюдента, полученный из нормального закона и законаc 2. Случайная величина t получается из дроби в числителе которой стоит случайная величина Z Гаусса с m=0 и s =1, а в знаменателе - случайная величина c 2 с n степенями свободы. По -прежнему при больших n закон Стьюдента переходит в нормальный закон (практически при n і 30). Но даже при небольших n вид кривой плотности распределения вероятностей для t очень похож на кривую 3 рис.1. Разница в том, что вместо s =1 для Z необходимо брать s =n /(n -2), т.е.среднее отклонение t от m=0 больше, чем среднее отклонение Z от m=0. Соответственно “холм” закона t более пологий, чем “холм” закона Z.
|